Instructional Unit

Investigating Centers of Triangles

This unit can be divided up as needed, but mainly focuses investigating the centers of triangles. Students can use technology to enhance their explorations, and even begin to draw their own conclusions based on their findings. To begin the unit, the students may be given a list of terms that will help them throughout the unit. Some of these terms may be review, while some terms will be seen for the first time during this unit. The terms may consist of the following:

· Midpoint

· Median

· Equidistant

· Co-linear

· Angle bisector

· Perpendicular bisector

· Altitude (of a triangle)

· Circumcenter

· Incenter

· Centroid

· Orthocenter

· Concurrent

· Euler Line

Once the students become familiar with the terms, they can use a program like GSP in order to construct the centers of triangles. For each construction, the students should start out with an arbitrary triangle. Then, the students can alter their arbitrary triangle into several types of triangles- equilateral triangles, isosceles triangles, etc. If the students are somewhat familiar with GSP, the constructions should be fairly simple.

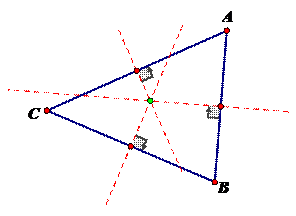
The teacher should play an active role in facilitating the discussions, incorporating the vocabulary given. When discussing the circumcenter, the following things should be discussed and explored:

· How is the circumcenter constructed?

· How does the circumcenter behave when the triangle is arbitrary, a right triangle, an equilateral triangle, or an isosceles?

· How could a circle be constructed using the circumcenter? Why is this possible?

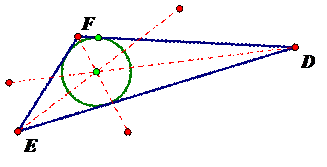
Some similar questions may be posed about the incenter:

· How is the incenter constructed?

· How does the incenter behave when the triangle is arbitrary, a right triangle, an equilateral triangle, or an isosceles?

· How could a circle be constructed using the incenter? Why is this possible?

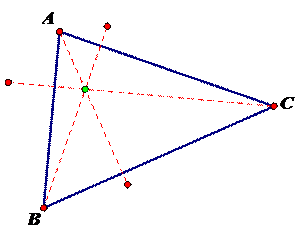
Some questions that might help explore the orthocenter could be:

· How is the orthocenter constructed?

· How does the orthocenter behave when the triangle is arbitrary, a right triangle, an equilateral triangle, or an isosceles?

Perhaps one of the most extensive explorations can be done when discussing the centroid. The centroid has some unique properties that the students may find very interesting.

First off, once the centroid is constructed, the students can explore the ratio between the longer segment and the shorter segment of the medians used in the construction. What is this ratio?

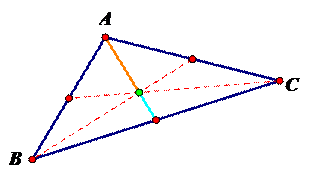
Secondly, what is the relationship between the triangles created by the medians used in the discussion? What do you notice about the area of the triangles created? For example, what can you conclude about the area of ΔAGD and ΔDGC? How do you know? (This is where line H comes into play!) What is the ratio between the area of ΔABD and ΔAGD? How do you know that this is the case?

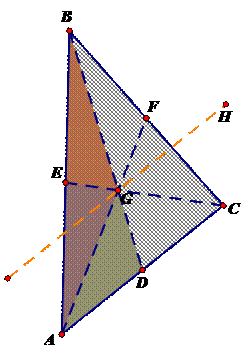
For another small exploration, the students should construct the centers of the triangles on the same equilateral triangle and on the same isosceles triangle. What happens with the centers of the equilateral triangle? What about the isosceles triangle? This is where the Euler line can be introduced.

Return to EMAT 4690/6690 Home page